旋转矩阵

发表于 | 分类于 |   |   次阅读

问题简述

本文研究几何变换矩阵，以及在 OpenCV 中实现图像的旋转、放缩。

旋转 $\theta$ 度

推导

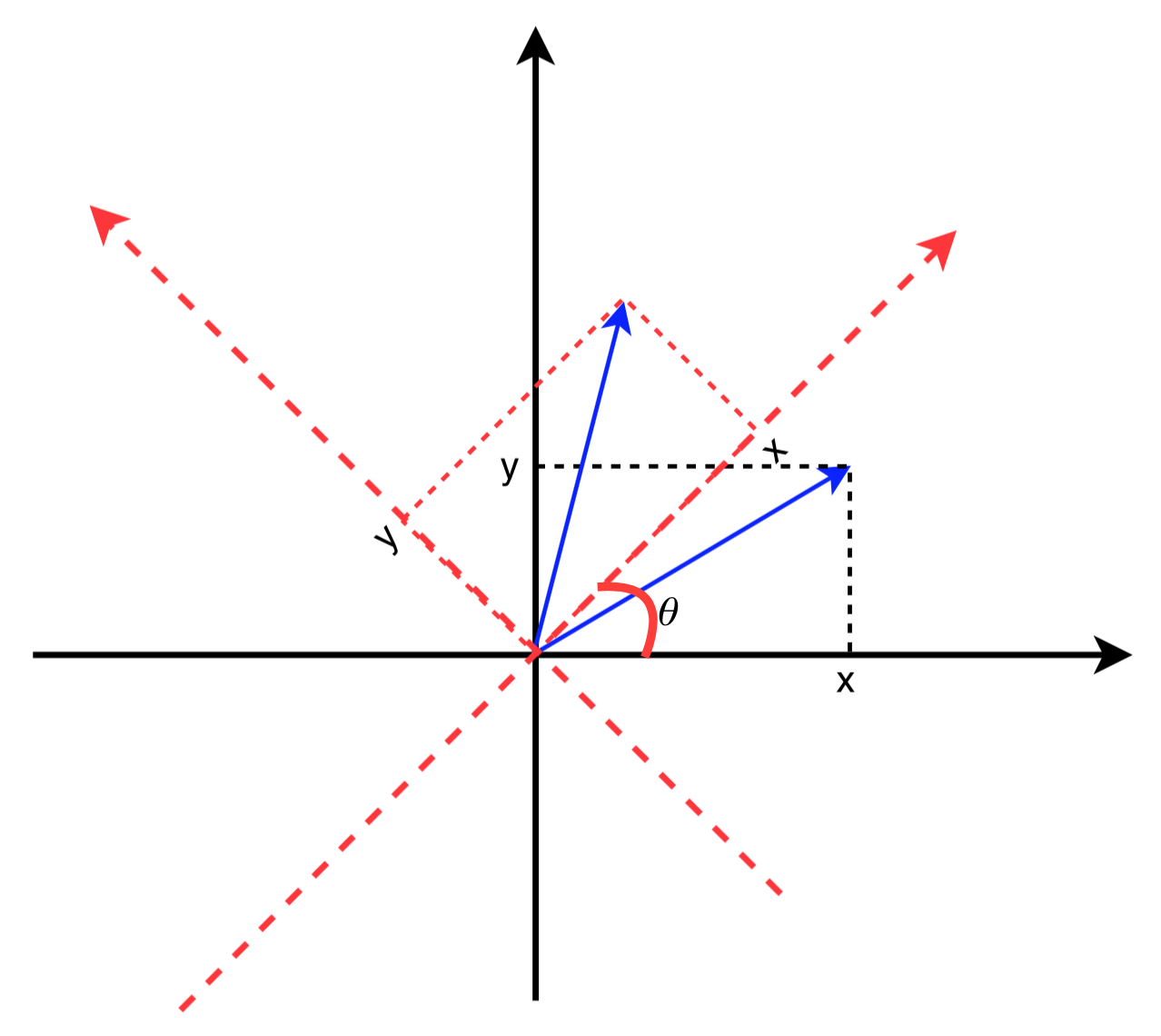
首先将问题简化：在二维坐标系中，将某点绕坐标原点旋转一定的角度，已知旋转前的坐标 $(x_0,y_0)$ 和旋转角 $\theta$，求旋转后的坐标 $(x,y)$。

如上图所示，旋转前后的目标点都用蓝色箭头表示，旋转前其坐标为 $(x, y)$ （推导过程为了区分，采用 $(x_0, y_0)$ ）。旋转前坐标系用黑色实线表示，为了辅助推导，图中作出了旋转后的坐标系，用红色虚线表示（可以想象成红色坐标系固连在点上，随着点一起旋转）。

原坐标系基底为:
$$
\vec b_1 = \left(
\begin{matrix}
1 \\
0
\end{matrix}
\right) \qquad
\vec b_2 = \left(
\begin{matrix}
0 \\
1
\end{matrix}
\right)
$$

原坐标表示成基底相加的形式：
$$
\left(
\begin{matrix}
x_0 \\
y_0
\end{matrix}
\right)=x_0\cdot\vec b_1+y_0\cdot\vec b_2 =
x_0\cdot\left(\begin{matrix}
1 \\
0
\end{matrix}\right)+y_0\cdot\left(\begin{matrix}
0 \\
1
\end{matrix}\right)
$$

从图中可以看到，旋转后的点与红色坐标系的相对位置没有改变，仍然等于 $x_0$ 个横向基底加 $y_0$ 个纵向基底。因此，只要求出红色坐标系的横向基底和纵向基底，即可获得旋转后的点在原坐标系中的坐标。根据三角函数，很容易得到这一组新的基底：
$$
\vec {b_1’} = \left(\begin{matrix}
cos\ \theta \\
sin\ \theta
\end{matrix}\right) \qquad
\vec {b_2’} = \left(\begin{matrix}
-sin\ \theta \\
cos\ \theta
\end{matrix}\right)
$$
因此，旋转后的点在原坐标系中的坐标为：
$$
\left(
\begin{matrix}
x \\
y
\end{matrix}
\right)=x_0\cdot\vec {b_1’}+y_0\cdot\vec {b_2’} =
x_0\cdot\left(\begin{matrix}
cos\ \theta \\
sin\ \theta
\end{matrix}\right)+y_0\cdot\left(\begin{matrix}
-sin\ \theta \\
cos\ \theta
\end{matrix}\right)
$$

转换成矩阵乘积的形式为：
$$
\left(
\begin{matrix}
x \\
y
\end{matrix}
\right) = \left[\begin{matrix}
cos\ \theta & -sin\ \theta \\
sin\ \theta & cos\ \theta
\end{matrix}\right]\cdot\left(\begin{matrix}
x_0 \\
y_0
\end{matrix}\right)
$$

OpenCV 旋转图片

若要在 OpenCV 中实现图片旋转，首先需要通过调用 cv2.getRotationMatrix2D 生成旋转矩阵，事实上，该矩阵同时涵盖了以任意点为中心的旋转（上一部分仅仅考虑了旋转中心为坐标原点的情况）+放缩变换。

1
2
3
4
5
img = cv2.imread('messi5.jpg',0)
rows,cols = img.shape
M = cv2.getRotationMatrix2D((cols/2,rows/2),90,1)
dst = cv2.warpAffine(img,M,(cols,rows))

cv2.getRotationMatrix2D 传入的参数分别为：旋转中心$(x_0, y_0)$，旋转角度 $\theta$（非弧度制），放缩量 $scale$。生成如下所示的矩阵：
$$
\left[\begin{matrix}
\alpha & \beta & (1-\alpha)\cdot x_0-\beta y_0 \\
-\beta & \alpha & \beta x_0+(1-\alpha)\cdot y_0
\end{matrix}\right]
$$

其中：
$$
\alpha = scale\cdot cos\theta \\
\beta = scale\cdot sin\theta
$$

分析上述矩阵中的元素，可以看出，$\alpha$、$\beta$ 是负责旋转的量。但是它的负号位置与第一部分推导的不同，这是因为图像坐标系不是标准坐标系，图像坐标系中规定图像左上角为坐标原点，水平向右为 $x$ 轴正方向，竖直向下为 $y$ 轴正方向。那么，OpenCV 又是如何把放缩和以任意点为中心的旋转整合到同一矩阵的呢？

其实可以把上述的复杂变换分解成几个简单变换：平移、放缩、旋转。

平移

旋转中心不是坐标原点的情况（i.e $(x_0, y_0)$），可以先将坐标原点临时平移到指定的旋转中心，然后进行旋转变换，再将坐标原点平移回去。可以想象成月球绕着地球转，先求出月球旋转某个角度后相对于地球的坐标，再根据地球的位置，求出月球相对于太阳的坐标。

平移矩阵为：
$$
T =
\left[\begin{matrix}
1 & 0 & -x_0 \\
0 & 1 & -y_0 \\
0 & 0 & 1
\end{matrix}\right]
$$
最后一行的目的是辅助计算，输入的坐标也增加一个维度，增加的维度上值始终为 1，例如 $[x, y]^T$ 变为 $[x, y, 1]^T$。

平移加放缩

坐标原点上的放缩矩阵为：

$$
S =
\left[\begin{matrix}
scale & 0 & 0 \\
0 & scale & 0 \\
0 & 0 & 1
\end{matrix}\right]
$$

若放缩中心不是坐标原点，则先将坐标系平移到放缩中心，放缩后再移回原点。这个过程可以用矩阵乘法表示：

$$
T’ST =
\left[\begin{matrix}
1 & 0 & x_0 \\
0 & 1 & y_0 \\
0 & 0 & 1
\end{matrix}\right]
\cdot
\left[\begin{matrix}
scale & 0 & 0 \\
0 & scale & 0 \\
0 & 0 & 1
\end{matrix}\right]
\cdot
\left[\begin{matrix}
1 & 0 & -x_0 \\
0 & 1 & -y_0 \\
0 & 0 & 1
\end{matrix}\right]
$$

平移加放缩加旋转

在上一节的过程中，移回坐标原点前，先进行一次旋转操作，就得到了平移加放缩加旋转的变换矩阵，也就是 OpenCV 中的变换矩阵。

图像坐标系中以坐标原点为中心的旋转矩阵为：

$$
R =
\left[\begin{matrix}
cos\ \theta & sin\ \theta & 0 \\
-sin\ \theta & cos\ \theta & 0 \\
0 & 0 & 1
\end{matrix}\right]
$$

因此，总的旋转矩阵为：

$$
T’RST =
\left[\begin{matrix}
1 & 0 & x_0 \\
0 & 1 & y_0 \\
0 & 0 & 1
\end{matrix}\right]
\cdot
\left[\begin{matrix}
cos\ \theta & sin\ \theta & 0 \\
-sin\ \theta & cos\ \theta & 0 \\
0 & 0 & 1
\end{matrix}\right]
\cdot
\left[\begin{matrix}
scale & 0 & 0 \\
0 & scale & 0 \\
0 & 0 & 1
\end{matrix}\right]
\cdot
\left[\begin{matrix}
1 & 0 & -x_0 \\
0 & 1 & -y_0 \\
0 & 0 & 1
\end{matrix}\right]
$$

也就是：

$$
\left[\begin{matrix}
scale\cdot cos\ \theta & scale\cdot sin\ \theta & x_0\cdot(1-scale\cdot cos\ \theta)-y_0\cdot scale\cdot sin\ \theta \\
-scale\cdot sin\ \theta & scale\cdot cos\ \theta & y_0\cdot(1-scale\cdot cos\ \theta)+x_0\cdot scale\cdot sin\ \theta \\
0 & 0 & 1
\end{matrix}\right]
$$

令

$$
\alpha = scale\cdot cos\theta \\
\beta = scale\cdot sin\theta
$$

得到
$$
\left[\begin{matrix}
\alpha & \beta & (1-\alpha)\cdot x_0-\beta y_0 \\
-\beta & \alpha & \beta x_0+(1-\alpha)\cdot y_0 \\
0 & 0 & 1
\end{matrix}\right]
$$
前两行与 OpenCV 文档中完全相同。

代码 1

可以直接调用 OpenCV 的函数对图片进行旋转，如下代码实现了将某幅图片绕其几何中心逆时针旋转 90°，并保持原尺寸。

1
2
3
4
5
6
7
8
9
10
11
import cv2
import matplotlib.pyplot as plt
img = cv2.imread('cat.jpg')
rows,cols = img.shape[0:2] # 图像的尺寸
M = cv2.getRotationMatrix2D((cols/2,rows/2),90,1) # 注意几何中心的坐标与尺寸的关系，横坐标对应列，纵坐标对应行
dst = cv2.warpAffine(img,M,(rows,cols)) # 注意目标图像的尺寸，这里 rows 和 cols 代表的是新图像在横、纵坐标方向的长度，不是原图中的行、列
 # 显示图片
dst = dst[:,:,::-1] # matplotlib 通道顺序为 RGB 而 OpenCV 通道顺序为 BGR 故在这里调整通道顺序
plt.imshow(dst)
plt.show()

代码 2

然而，当利用上述代码旋转矩形图像时，会出现旋转后的图片有黑边的现象。这是由于旋转后的图像中心与旋转前的图像中心在旋转前的图像坐标系中不重合的缘故。具体来讲，旋转前的图像中心坐标为(cols/2, rows/2)，以90°旋转为例，旋转后的图像中心坐标为(rows/2, cols/2)。因此需要再乘以一个平移矩阵，横向平移量为 rows/2-cols/2，纵向平移量为 cols/2-rows/2。由于矩阵乘法很耗运算资源，而乘以平移矩阵的结果一目了然，因此在代码实现过程中，直接修改旋转矩阵第一行和第二行第三列的元素值即可。

下面的代码适用于任意角度的旋转。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
import cv2
import matplotlib.pyplot as plt
import numpy as np
I = cv2.imread('cat.jpeg')
height, width = I.shape[0:2]
center = (width/2, height/2)
theta = np.pi*1.7
scale = 1
rot_mat = cv2.getRotationMatrix2D(center, np.degrees(theta), scale)
 # rot_mat = np.vstack((rot_mat, [0,0,1]))
new_height = height*np.abs(np.cos(theta))+width*np.abs(np.sin(theta))
new_width = height*np.abs(np.sin(theta))+width*np.abs(np.cos(theta))
new_center = (new_width/2, new_height/2)
dx, dy = (new_center[0]-center[0], new_center[1]-center[1])
 #trans_mat = np.eye(3)
 #trans_mat[0,2] = dx
 #trans_mat[1,2] = dy
 #affine_mat = np.dot(trans_mat, rot_mat)
affine_mat = rot_mat[0:2,:]
affine_mat[0,2] += dx
affine_mat[1,2] += dy
J = cv2.warpAffine(I, affine_mat, (int(new_width), int(new_height)))
plt.imshow(I)
plt.show()
plt.imshow(J)
plt.show()

参考资料

Geometric Transformations of Images